Proximity sets (proxets)
In computer programs, the data structures are usually declared upfront, explicitly or implicitly, and their meaning is stipulated before the computation begins. In network computation, on the other hand, there are usually no global declarations, and each network node can interpret the shared data differently. This is, of course, the familiar technical problem of Semantic Web, and of the Web search. But note that it is also a very basic problem of human communication: e.g., if I say that I love romantic comedies, and you say that you love romantic comedies, we may mean completely different things. How do we find a common ground?
In a computer, information processing usually boils down to data transformation: a computer inputs some numbers, and outputs some other numbers. In a network, information can also be processed through data distribution: e.g., if a photo is uploaded to a web site and it reappears at a million other web sites, it becomes a concept, connecting these sites. Assigning the meaning to data is thus an ongoing 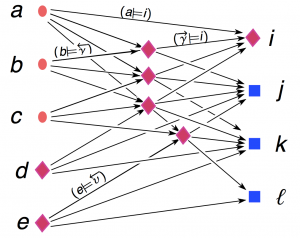 process in a network, supported by the network services, search, classification, naming, routing. People share their ideas and concepts with each other, and the network generates new ideas and concepts. These new concepts are the dark matter of networks: they are only observable through their “gravitational” effects, increasing the proximity among the other concepts. How can we mine this dark matter?
process in a network, supported by the network services, search, classification, naming, routing. People share their ideas and concepts with each other, and the network generates new ideas and concepts. These new concepts are the dark matter of networks: they are only observable through their “gravitational” effects, increasing the proximity among the other concepts. How can we mine this dark matter? 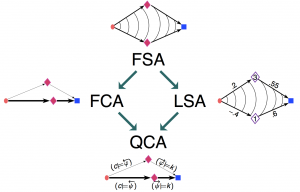
Taken together, the problems of semantics of computation and of information extraction span a space with many new dimensions. The logical problems blend with the problems of learning, information retrieval, and data analysis. As a frame of reference, we took a unified mathematical framework, subsuming the various spectral decomposition methods of network analysis, such as Latent Semantic Indexing (LSI) and Formal Concept Analysis (FCA). This mathematical framework opens an alley towards a new approach to concept analysis, based on a remarkably simple mathematical structure of proximity sets (proxets), which generalize partially ordered sets (posets).
This project is at an early stage, but the following papers provide some background:

