Most people would say that security is an engineering problem: you set up a web site and you want to make sure that it is not abused; or you build a house and you don’t want it to be burglarized. We usually expect engineers to assure such security requirements. Why are we hammering on security science here?
What is the difference between science and engineering?
Here is an answer going back to what was probably the very first paper on formal methods, Tony Hoare’s ‘Programs are Predicates’:
It is the aim of the natural scientist to discover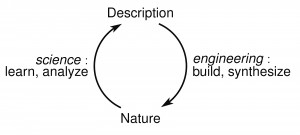 
mathematical theories, formally expressed as predicates describing the relevant observations that can be made of some physical system. […]
The aim of an engineer is complementary to that of the scientist. He starts with a specification, formally expressible as a predicate describing the desired observable behaviour of a system or product not yet in existence. Then […] he must design and construct a product that meets that specification.
The picture on the right (not from the paper) illustrates the point:
- engineers build artificial systems,
- scientists analyze natural systems.
Is security the subject of a science or an engineering task?
Security is a property of artificial systems: software, a house, a car. So the case seems clear: security is an engineering task.
However, drug are usually synthesized, and thus artificial, yet their effects are analyzed scientifically. A car is built by engineers, but its safety and security are analyzed by scientific methods. The Web consists of programs, written by engineers, but the processes that it supports are usually not programmable or controllable, but need to be analyzed by scientific methods. For all practical purposes, web computation can be considered to be a natural process, just like genetic computation and natural selection.
So security is both an engineering task, and the subject of a science.
So that is that. Except there is a different, less obvious and more interesting link of security and science.
Security is like science
The glorious view of science is that it provides the eternal laws of nature. This view was persuasively expressed by David Hilbert, one of the most influential mathematicians of XIX and XX centuries, in his famous Koenigsberg address of 1930:
For the mathematician there is no Ignorabimus, and, in my opinion, not at all for natural science either. The true reason why [no one] has succeeded in finding an unsolvable problem is, in my opinion, that there is no unsolvable problem. In contrast to the foolish Ignorabimus, our credo avers: We must know, We shall know!
In a particular feat of historic irony, at that same conference young Kurt Goedel announced his famous incompleteness theorem, providing a method to generate unsolvable problems. Although not many people paid attention to Goedel during the conference, it soon became clear that Hilbert’s Program of discovering eternal laws was dead.
The practice and the theory of XX century science demonstrated that the glorious view of science was essentially wrong, i.e. completely wrongheaded, in the sense that it is the very essence of science that it never provides enternal laws, but only transient laws, which it continues to test, to disprove and to improve. This transience of scientific theories is nowadays both the generally accepted foundation of logic of scientific discovery for the scientists, as well as perhaps the best kept secret of science for the general public.
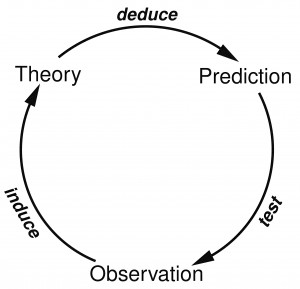
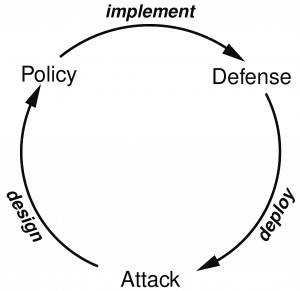
This is where the parallel between science and security emerges. It is reflected in two following columns.
The quote in the left column is from Richard Feynman’s ‘Lectures on the Character of Physical Law’ (which were also recorded). On paragraph in the left column is the analogous statement about the character of security claims. Just like science, security never settles. The ongoing of processes science and the ongoing processes of security follow the same logical process, looping as in the next two diagrams.
But what are the practical consequences of this analogy? One direction for applying scientific methods in security is described in my HoTSoS paper (also on arxiv). A broader approach is the SecSci effort here.
Authenticity vs integrity
Most people do not use the terms “authenticity” and “integrity” as synonyms, but the differences between the two concepts as used in security research differ in varied and often confusing ways. A message is authentic when its origin claim is true: e.g., a painting is authentic if when it says “I was painted by Picasso”, then it was really painted by Picasso. Integrity usually means that the message was not altered in transfer: e.g., the integrity of a painting can be destroyed if it is changed in restoration. The integrity of a voting ballot can be destroyed if the tamper protections on it are damaged, since we cannot be sure any more whether the vote was altered or not. Some people call the process of establishing authenticity “entity authentication”, and the process of establishing integrity “message authentication”. Both processes require that something that we observe (e.g. a painting) allows us to draw conclusions about something that we cannot observe (who made the painting). Deriving what is unobservable from what is observable is a formidable logical task: in a sense, both science and religion are can be viewed as methods for authentication. More about this later.
Secrecy vs confidentiality
The terms “secrecy” and “confidentiality” are also used in subtly different ways, but they both express restrictions on some undesired information flows. E.g., a medical file is confidential, in the sense that its contents can only be disclosed to the patient and to the physician, although everyone knows that the file surely exists; an intelligence file about a suspect is secret, in the sense that even its existence cannot be disclosed. To make it more complicated, even the term “privacy” is often used in related senses: e.g., contrast a private ceremony with a secret ceremony.
Think about concepts, not words
Without the formal definitions, the security terminology is used freely and imprecisely in everyday life, and there is nothing wrong with that. In security research, though, it is useful to fix some definitions, to assign some words to some concepts, and to stick with them even if other people may use the words differently. Our goal is not to study the ways people use the words “confidentiality” and “integrity”, but to understand and develop some methods to restrict the undesired data flows, and to establish the desired data flows.
So lets stick with the taxonomy of the security concepts, proposed in this post.
CIA or CIAA?
In many security courses and overviews, you will encounter the CIA triad, referring to Confidentiality, Integrity and Availability. This triad consists of three of the four basic security concepts that we spelled out in SecSci taxonomy. They are displayed on a triangle, clarified by examples, and often related with other concepts, such as trustworthiness or reliability, assumed to be intuitively clearer than confidentiality, integrity. or availability. Students often wonder why are these three more important, and whether there might be other important security properties that we still didn’t encounter, and some authors extend the triad by their favorites, such as Non-repudiation, so that CIA becomes CIAN. Then the students ask whether there might still other important security properties, and there is no obvious reason why the list should ever end.
The taxonomy above can be viewed as the triad extended by Authorization, so that CIA became CIAA. What is the point of that? Well, if security research is concerned with what-you-know (information) or what-you-have (resources), and its goals are either to prevent bad things or to provide good things, then there are just 4 security goals: Confidentiality and Integrity of what-you-know, and Authorization and Availability of what-you-have. And you know that the CIAA list is complete and exhaustive, and that any imaginable security must be a combination of those 4.
Spelling out the informal security concepts and the principles tried out in practice has been a useful and important strategy in the engineering approach to security, where we gather experience to build better and better systems. But a scientific approach to security, necessary for dealing with systems that combine engineered and natural processes, requires that we precisely define the subject of our science. To do that, we need an exhaustive list of security properties: a taxonomy which covers not only the properties that we have encountered, but also the properties that we have not yet thought about, but may encounter in the future. The good-things/bad-things taxonomy seems like a good candiate for that purpose. It played a similar role in software science, so maybe it will get us ahead in security science as well.
So whenever you encounter the CIA triad, then either expand it to CIAA, or maybe even ignore the whole thing.
To know, to have, or to be
What kinds of things need to be secured? What kinds of things can be used to secure what needs to be secured?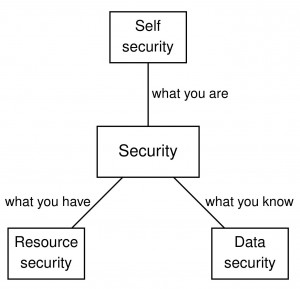 
There is a slogan that security is based on three kinds of things:
- what you know: passwords, digital keys…
- what you have: smartcards, physical keys…
- what you are: fingerprints, handwriting…
How do we know that there are no other kinds things? We know because there are just three ways of sharing things:
- What I know I can copy and give it to you, so that we both know it. (We call such things data.)
- What I have I cannot copy, but I can give it to you, so that you have it and I don’t. (We call such things objects or resources.)
- What I am I cannot either copy or give to you, and only I am me. (We call what such things identity or self.)
Please don’t get confused by the fact that smartcards can be cloned and that biometric properties can be faked. The point is here that copying data is essentially costless, whereas copying smartcards or cloning people is not. CDs and DVDs can also be copied, but the music and the film industries were thriving with that problem, and they have badly suffered from the costless data streams.
Basic security properties and goals
At the highest level, security research is subdivided into studying the resource security of what-you-have, and the data security of what-you-know. A crude taxonomy of the security properties studied in these two areas is on the picture below.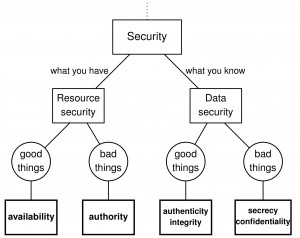
- Within resource security, the requirement that the good resource uses do happen is called availability; the prevention of the bad resource uses is called authorization.
- Within data security, the requirement that the good data flows do happen is called authenticity, or integrity; the prevention of the bad data flows is called secrecy, or confidentiality.
There are, of course, many different ways to use the same words, and many people use the words “confidentiality”, “integrity” etc, in ways not covered by the above taxonomy. But we need some definitions, and these seem useful. See this post for more.
What about the third branch: self security of what-you-are?
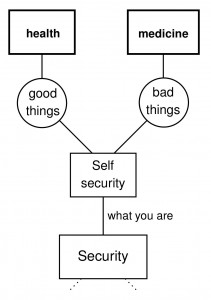For better or for worse, that’s what they study in medicine and health sciences. Security research still didn’t really connect up with that area, although some biometric researchers of course study what-you-are. There have been various efforts towards biologically inspired security and towards viewing security as immunity. But the real relations between what-you-know and what-you-have and what-you-are are still waiting to be clarified ;)
Security is many things for many people. For a general, security is national security. For a child, security means that there are no bullies at school or in the computer. For a banker, security is a protected financial asset, structured so that the risks are minimized or tranferred to someone else. For a bee, security means that anyone who tries to steal honey will get bee’s sting, even if it costs her life. There are many different views of security.
The different views lead to a lot of confusion. A security strategy recommended to a child (e.g., “Do not escalate conflicts”) may not be accepted in national security, and may again be universally recommended for a workplace, even within a department of national security. Difficult problems of cyber security are often easily solved in everyday life, and the other way around.
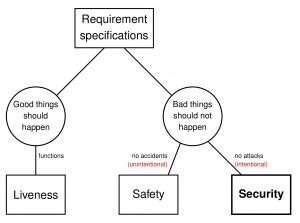
Security is one of the three basic families of goals that we strive for every day. First of all, we split our goals into two families of requirements:
- that good things should happen, and
- that bad things should not happen.
And then there are two kinds of bad things, which we treat differently:
- natural hazards, and
- intentional attacks.
The requirement that good things should be guaranteed to eventually happen is called liveness. The requirement that we should be protected against natural hazards are called safety. The requirement that we should be protected against intentional attacks is called security. Here is a picture. (Click to enlarge.)
Let us look at some examples.
- The main function of a house is to provide a space for sleeping, a space for cooking, etc. These are its liveness properties. The door on the house protects us from natural hazards, and thus provides safety. The lock on the door protects us from thieves, and thus provides security.
- The main function of a car is to drive from place to place. A working engine is necessary for this liveness property. The brakes are necessary for safety, as they allow us to prevent some accidents. The alarm system is necessary for security, as it prevents theft.
- The main function of a text editing application is to let us edit text. Its liveness requires that it saves the changes that we make. Its safety requires that it does not crash or deadlock because of the software bugs left behind careless programmers, like buffer overflows, null pointers, etc. The security of a text editor requires that it does not let attackers take control of our data or computer. Note that a safety failure can cause a security failure: e.g., an attacker can use a buffer overflow to install malware.
Hello world
and aloha SecSci students of University of Hawaii. In this blog I (dusko, and I hope other aseconauts as well) will try to flesh out the basic ideas about security, as studied in the Security Science Courses, and in general. The complete course materials are available through laulima. Comments and questions are welcome.
Why are we interested in security?
Surely not all for the same reason. Some people like it because hacking is so cool. Others are interested in nice security jobs. Yet others want to understand security threats that rage in cyber space, and in real life.
But beyond and below all of different views of security, there is a simple common denominator: Security is about people lying and cheating each other. They steal each other’s secrets and money, they impersonate each other, they want to outsmart each other. What can be more fun than that? Or what can be more fun than preventing that?
But how can I prevent people who are smarter than me from outsmarting me? This is where science comes in. Science looks for ways to do things by method, and not by cleverness. When you solve a problem by cleverness, it does not make the next problem any easier; when you solve a problem by method, then the next problem becomes easier, because you have learned the method. That is why security is like science: you never completely achieve the goal, but you build new results based on the old results, and they keep getting better. We’ll get to a general model and concrete examples later. If you don’t want to wait but want to get an idea about this now, you could have a look into my paper about trust building as hypothesis testing, published here.