Monoidal computer
Explorations into security by obscurity led us to the task to measure the logical distance between algorithms (or more precisely, to measure the logical hardness of constructing an attack from some given knowledge about the system). This task led us to explore certain refinements of Bennett‘s concept of logical depth, and to start thinking about possible security applications of algorithmic information theory in general. However, it soon became clear that, even if we could find a completely satisfactory general concept of logical distance of algorithms, measuring the distance of a specific pair of algorithms would boil down to estimating the lower bounds on complexity of Turing Machines needed to generate some other Turing Machines. That looked like a rather hopeless task: machine programming of machine program generators.
Monoidal computer is an effort to circumvent this problem, by providing a high level language for reasoning about 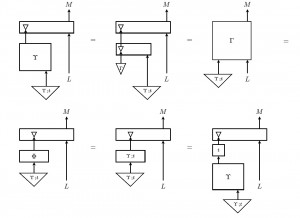 computability in complexity, in contrast with the low level languages, like Turing Machines, lambda calculus, Post systems etc. Monoidal computer is thus a new model of computation, described in terms of monoidal categories. It conforms the Church-Turing Thesis, and captures the same computable functions as the standard models. It provides a succinct categorical interface to most of them, free of their diverse implementation details, using the ideas and structures that in the meantime emerged from research in semantics of computation and programming. The salient feature of the language of monoidal categories is that it is supported by a sound and complete graphical formalism, string diagrams, which provide a concrete and intuitive interface for abstract reasoning about computation. E.g., on the right is a diagrammatic proof of Kleene’s Second Recursion Theorem, the pinnacle of computability theory.
computability in complexity, in contrast with the low level languages, like Turing Machines, lambda calculus, Post systems etc. Monoidal computer is thus a new model of computation, described in terms of monoidal categories. It conforms the Church-Turing Thesis, and captures the same computable functions as the standard models. It provides a succinct categorical interface to most of them, free of their diverse implementation details, using the ideas and structures that in the meantime emerged from research in semantics of computation and programming. The salient feature of the language of monoidal categories is that it is supported by a sound and complete graphical formalism, string diagrams, which provide a concrete and intuitive interface for abstract reasoning about computation. E.g., on the right is a diagrammatic proof of Kleene’s Second Recursion Theorem, the pinnacle of computability theory.
The goal of this effort is to provide a convenient high level programming language for a theory of computational and cryptographic resources, such as one-way functions, and trapdoor functions, by adopting the methods for hiding the low level implementation details that emerged from practice. The first paper (of the planned series of four) is

